Apakah yang dimaksud bangun datar? Pertanyaan ini membuka pintu ke dunia geometri yang menakjubkan, tempat bentuk dan ruang berinteraksi dalam harmoni. Mari kita selami bersama, menjelajahi esensi dari bangun datar, mulai dari definisi fundamental hingga aplikasi praktis yang tak terhitung jumlahnya.
Bangun datar adalah fondasi dari banyak konsep matematika dan memiliki peran penting dalam kehidupan sehari-hari. Dari segitiga sederhana hingga lingkaran yang rumit, setiap bentuk memiliki karakteristik unik yang membuatnya menarik untuk dipelajari. Pemahaman tentang bangun datar membuka wawasan tentang dunia visual di sekitar kita, memungkinkan kita untuk menganalisis, merancang, dan menciptakan dengan lebih efektif.
Memahami Esensi Bangun Datar
Source: tuliskan.id
Mari kita selami dunia geometri, tempat bentuk dan ruang berinteraksi dalam harmoni yang menakjubkan. Kita akan memulai perjalanan eksplorasi dengan memahami konsep fundamental yang menjadi pijakan bagi pemahaman kita tentang dunia visual: bangun datar. Pemahaman yang kuat tentang bangun datar bukan hanya tentang menghafal definisi, tetapi juga tentang mengapresiasi keindahan dan keteraturan yang tersembunyi di balik setiap bentuk. Bersiaplah untuk membuka mata terhadap dunia geometri yang lebih luas!
Definisi Komprehensif Bangun Datar
Bangun datar adalah entitas geometri dua dimensi yang memiliki panjang dan lebar, namun tidak memiliki ketebalan atau kedalaman. Mereka terbatas oleh garis lurus atau kurva, dan sepenuhnya terletak pada satu bidang. Ciri utama yang membedakan bangun datar adalah keberadaannya dalam dua dimensi. Ini berbeda dengan bangun ruang, yang menempati ruang tiga dimensi dan memiliki volume. Bangun datar memiliki luas, yang mengukur area yang ditempati oleh bentuk tersebut, serta keliling, yang mengukur panjang batas luarnya.
Contoh umum bangun datar meliputi segitiga, persegi, lingkaran, dan berbagai poligon lainnya. Pemahaman mendalam tentang bangun datar membuka pintu menuju pemahaman konsep geometri yang lebih kompleks.
Perbandingan Karakteristik Bangun Datar dan Bangun Ruang
Memahami perbedaan antara bangun datar dan bangun ruang sangat penting. Tabel berikut mengilustrasikan perbedaan mendasar antara keduanya:
| Karakteristik | Bangun Datar | Bangun Ruang | Contoh | |
|---|---|---|---|---|
| Dimensi | 2 (Panjang, Lebar) | 3 (Panjang, Lebar, Tinggi/Kedalaman) | Segitiga, Persegi, Lingkaran | Kubus, Balok, Bola |
| Bidang | Terletak pada satu bidang | Menempati ruang | Satu bidang datar | Beberapa bidang, membentuk volume |
| Sifat | Memiliki luas dan keliling | Memiliki volume, luas permukaan, dan dapat memiliki keliling (pada penampang) | Luas = πr², Keliling = 2πr | Volume = πr²h, Luas Permukaan = 2πr(r+h) |
Pandangan Ahli Matematika tentang Bangun Datar
Para ahli matematika telah lama mengakui pentingnya bangun datar sebagai fondasi geometri. Berikut adalah beberapa kutipan yang merangkum pandangan mereka:
“Geometri adalah studi tentang bentuk dan ruang, dan bangun datar adalah blok bangunan dasar dari pemahaman kita tentang keduanya.”
-Euclid (Sumber: Elements)“Memahami bangun datar adalah kunci untuk memahami konsep geometri yang lebih kompleks, seperti trigonometri dan kalkulus.”
-Rene Descartes (Sumber: La Géométrie)“Bangun datar memberikan kerangka kerja yang kuat untuk memahami dunia di sekitar kita, dari desain arsitektur hingga seni visual.”
-Pythagoras (Sumber: Teorema Pythagoras)
Pandangan para ahli ini menekankan relevansi bangun datar dalam pembelajaran geometri. Mereka adalah dasar untuk membangun pemahaman yang lebih mendalam tentang konsep matematika lainnya.
Ilustrasi Berbagai Contoh Bangun Datar
Mari kita visualisasikan beberapa contoh bangun datar dasar:
- Segitiga: Sebuah bangun datar yang dibatasi oleh tiga sisi dan tiga sudut. Contohnya termasuk segitiga sama sisi (semua sisi sama panjang), segitiga sama kaki (dua sisi sama panjang), dan segitiga siku-siku (salah satu sudutnya 90 derajat). Elemen penting meliputi sisi, sudut, dan titik pusat (titik pertemuan garis tinggi).
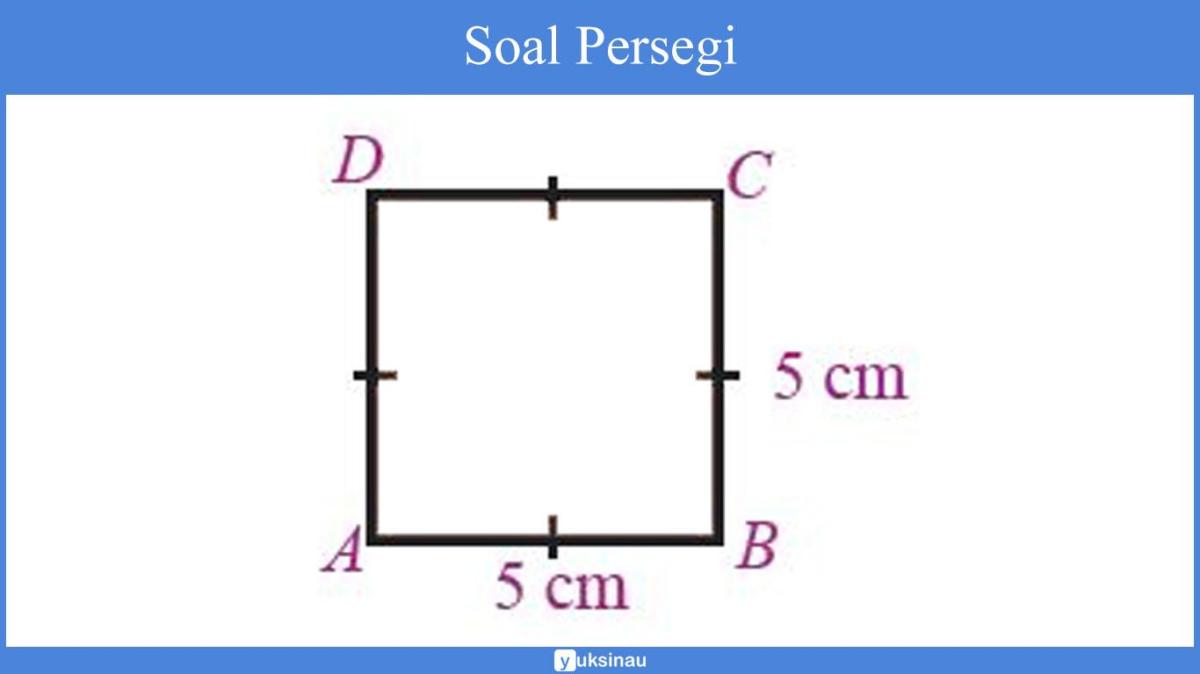
- Persegi: Sebuah bangun datar dengan empat sisi yang sama panjang dan empat sudut siku-siku. Elemen penting meliputi sisi, sudut, diagonal (garis yang menghubungkan dua sudut yang berhadapan), dan titik pusat.
- Lingkaran: Sebuah bangun datar yang dibatasi oleh kurva tertutup yang disebut keliling, dengan setiap titik pada keliling berjarak sama dari titik pusat. Elemen penting meliputi jari-jari (jarak dari pusat ke keliling), diameter (garis yang melewati pusat dan menghubungkan dua titik pada keliling), dan pusat.
- Persegi Panjang: Sebuah bangun datar dengan empat sisi, di mana sisi yang berhadapan sama panjang dan sejajar, serta empat sudut siku-siku. Elemen penting meliputi panjang, lebar, dan titik pusat.
Ilustrasi ini membantu memperjelas karakteristik dan elemen penting dari masing-masing bangun datar.
Bangun Datar sebagai Fondasi Konsep Geometri yang Lebih Kompleks
Konsep “bangun datar” adalah fondasi penting dalam pengembangan konsep geometri yang lebih kompleks. Memahami bangun datar membuka jalan bagi pemahaman luas dan volume, konsep yang sangat penting dalam matematika dan ilmu pengetahuan. Misalnya, untuk menghitung luas permukaan sebuah bangun ruang seperti kubus atau balok, kita perlu memahami luas bangun datar yang membentuk sisi-sisi bangun ruang tersebut. Konsep keliling dan luas bangun datar menjadi dasar untuk memahami konsep turunan dalam kalkulus.
Aplikasi bangun datar sangat luas, mulai dari perhitungan area tanah, perencanaan konstruksi bangunan, hingga desain grafis dan animasi. Penguasaan konsep bangun datar adalah langkah awal yang krusial dalam menguasai geometri secara keseluruhan, membuka pintu menuju pemahaman yang lebih mendalam tentang dunia di sekitar kita.
Menjelajahi Klasifikasi
Dunia bangun datar adalah kanvas tak terbatas bagi imajinasi dan logika. Memahami bagaimana kita mengelompokkan dan mengenali bentuk-bentuk ini membuka pintu menuju pemahaman yang lebih dalam tentang dunia di sekitar kita. Mari kita selami dunia bangun datar, dari yang paling sederhana hingga yang paling memukau, dan temukan bagaimana mereka membentuk dasar dari banyak aspek kehidupan kita.
Mari kita mulai petualangan pengetahuan! Tahukah kamu, gaya kupu-kupu disebut juga dengan istilah yang seringkali tak asing di telinga para perenang? Ini adalah kunci untuk menguasai kolam. Sekarang, mari kita beralih ke sesuatu yang lebih nyata, seperti contoh teks eksplanasi adalah gerbang menuju pemahaman dunia sekitar, sangat menarik, bukan? Dan jangan lupakan keajaiban gerak pada tumbuhan , sebuah tarian kehidupan yang menakjubkan.
Akhirnya, mari kita nikmati alunan merdu alat musik dari Maluku , yang akan membawamu ke dunia penuh warna!
Setiap bangun datar memiliki karakter unik yang membedakannya. Dengan mengidentifikasi ciri-ciri ini, kita tidak hanya meningkatkan kemampuan visual kita, tetapi juga memperkuat kemampuan berpikir analitis. Mari kita mulai perjalanan yang mengasyikkan ini!
Ragam Jenis Bangun Datar dan Karakternya
Klasifikasi bangun datar adalah kunci untuk menguasai geometri. Dari bentuk dasar hingga yang lebih kompleks, setiap kategori memiliki karakteristik yang membedakannya. Berikut adalah beberapa contoh yang akan membuka wawasan Anda:
Segi banyak adalah fondasi. Mereka adalah bangun datar tertutup yang dibatasi oleh sisi-sisi lurus. Contohnya adalah segitiga, persegi, pentagon, dan seterusnya. Mereka berbeda dalam jumlah sisi dan sudut. Lingkaran adalah bangun datar yang unik, didefinisikan oleh jarak konstan dari titik pusat ke setiap titik pada kelilingnya.
Turunannya termasuk elips dan parabola, yang muncul dalam banyak aplikasi praktis.
Contoh konkret:
- Segitiga: Bangun datar dengan tiga sisi dan tiga sudut. Contohnya adalah segitiga sama sisi, segitiga sama kaki, dan segitiga siku-siku.
- Persegi: Segi empat dengan empat sisi yang sama panjang dan empat sudut siku-siku.
- Segilima: Segi banyak dengan lima sisi.
- Lingkaran: Bangun datar yang semua titiknya berjarak sama dari titik pusat.
- Elips: Bentuk oval yang dihasilkan dari pemotongan kerucut.
Perbedaan Utama Antara Segi Banyak
Memahami perbedaan antara berbagai jenis segi banyak adalah kunci untuk menguasai geometri. Mari kita bedah perbedaan utama mereka:
- Segitiga:
- Jumlah Sisi: 3
- Jumlah Sudut: 3
- Sifat: Jumlah sudut selalu 180 derajat.
- Persegi:
- Jumlah Sisi: 4
- Jumlah Sudut: 4 (semua 90 derajat)
- Sifat: Semua sisi sama panjang, sudut siku-siku, diagonal sama panjang dan saling berpotongan di tengah.
- Segilima:
- Jumlah Sisi: 5
- Jumlah Sudut: 5
- Sifat: Jumlah sudut internal 540 derajat.
- Segi Enam:
- Jumlah Sisi: 6
- Jumlah Sudut: 6
- Sifat: Jumlah sudut internal 720 derajat.
- Segi Delapan:
- Jumlah Sisi: 8
- Jumlah Sudut: 8
- Sifat: Jumlah sudut internal 1080 derajat.
Klasifikasi Bangun Datar dalam Pemecahan Masalah Geometri
Klasifikasi bangun datar bukan hanya teori; ia adalah alat ampuh untuk memecahkan masalah geometri. Dengan mengidentifikasi jenis bangun datar, kita dapat menerapkan rumus dan teorema yang relevan untuk menemukan luas, keliling, sudut, dan sifat-sifat lainnya.
Contoh Studi Kasus:
Bayangkan seorang arsitek yang merancang sebuah rumah. Ia perlu menghitung luas atap yang berbentuk trapesium untuk menentukan jumlah genteng yang dibutuhkan. Dengan mengidentifikasi bentuk tersebut sebagai trapesium, ia dapat menggunakan rumus luas trapesium (1/2
– (alas1 + alas2)
– tinggi) untuk menghitung luasnya. Begitu pula, dalam bidang teknik, seorang insinyur harus menghitung volume sebuah tangki berbentuk silinder. Dengan memahami bahwa tangki tersebut adalah silinder, ia dapat menggunakan rumus volume silinder (π
– r^2
– tinggi) untuk menghitung volume tangki.
Contoh lain adalah dalam desain taman, seorang perancang lansekap perlu menghitung luas area yang akan ditanami rumput. Dengan mengidentifikasi bentuk area tersebut, misalnya persegi panjang atau lingkaran, perancang dapat menggunakan rumus luas yang sesuai untuk menentukan jumlah rumput yang dibutuhkan.
Contoh lain adalah dalam navigasi, memahami bentuk dan sifat segitiga sangat penting untuk menghitung jarak dan sudut. Dalam seni, klasifikasi bangun datar membantu seniman dalam komposisi dan proporsi. Dalam kehidupan sehari-hari, pemahaman tentang bangun datar memungkinkan kita untuk mengoptimalkan penggunaan ruang, merencanakan proyek, dan memahami dunia visual di sekitar kita.
Perbandingan Visual Berbagai Jenis Bangun Datar
Mari kita visualisasikan perbedaan antara berbagai jenis bangun datar. Perhatikan bagaimana jumlah sisi, bentuk sudut, dan simetri menciptakan perbedaan visual yang signifikan.
Segitiga: Tiga sisi, tiga sudut, bentuk yang beragam (siku-siku, lancip, tumpul, sama sisi, sama kaki). Tidak selalu simetris, kecuali segitiga sama sisi atau sama kaki.
Persegi: Empat sisi yang sama panjang, empat sudut siku-siku. Sangat simetris, dengan dua sumbu simetri yang berpotongan di tengah.
Segilima: Lima sisi, lima sudut. Bentuknya bisa beragam, namun segilima beraturan memiliki sisi dan sudut yang sama. Memiliki simetri rotasi.
Lingkaran: Tidak memiliki sisi, hanya memiliki satu keliling. Semua titik pada keliling berjarak sama dari pusat. Sangat simetris, dengan tak terhingga sumbu simetri.
Elips: Bentuk oval. Memiliki dua sumbu simetri.
Perbedaan ini sangat penting dalam mengenali dan memahami sifat-sifat setiap bangun datar.
Peran Klasifikasi Bangun Datar dalam Kehidupan Sehari-hari
Pemahaman tentang klasifikasi bangun datar jauh lebih dari sekadar pelajaran di sekolah. Ia memainkan peran penting dalam banyak aspek kehidupan sehari-hari.
Dalam desain arsitektur, pengetahuan tentang bentuk dan sifat bangun datar sangat penting. Arsitek menggunakan konsep ini untuk merancang bangunan yang estetis dan fungsional. Dalam seni, seniman menggunakan bangun datar sebagai elemen dasar dalam komposisi mereka. Pemahaman tentang proporsi, simetri, dan keseimbangan memungkinkan mereka menciptakan karya seni yang menarik. Dalam teknologi, pemahaman tentang bangun datar digunakan dalam berbagai aplikasi, mulai dari desain chip komputer hingga pembuatan robot.
Dalam dunia nyata, kita melihat bangun datar dalam berbagai bentuk, dari jalan raya hingga kemasan produk. Kemampuan untuk mengenali dan memahami bentuk-bentuk ini membantu kita memahami dunia di sekitar kita dengan lebih baik.
Menggali Sifat-Sifat Unik
Mari kita selami dunia bangun datar, bukan hanya sebagai bentuk visual, tetapi sebagai kunci untuk membuka rahasia alam semesta. Memahami sifat-sifat unik setiap bangun datar adalah seperti memegang peta harta karun, yang akan membimbing kita melewati labirin masalah dan tantangan. Setiap garis, sudut, dan kurva menyimpan potensi tak terbatas, siap untuk diungkap dan dimanfaatkan. Bersiaplah untuk terpukau oleh keajaiban matematika yang tersembunyi di balik kesederhanaan bangun datar.
Sifat-Sifat Unik Bangun Datar Utama
Setiap bangun datar memiliki karakter yang khas, seperti sidik jari yang membedakannya dari yang lain. Segitiga, persegi, dan lingkaran, masing-masing menawarkan keunikan yang memengaruhi cara kita memandang dan berinteraksi dengan dunia di sekitar kita.
- Segitiga: Bangun datar paling sederhana namun fundamental. Sifat uniknya terletak pada hubungan antara ketiga sisinya dan sudutnya. Jumlah sudut dalam segitiga selalu 180 derajat. Luas segitiga dapat dihitung dengan rumus
Luas = 1/2
– alas
– tinggi. Contohnya, jika sebuah segitiga memiliki alas 10 cm dan tinggi 5 cm, maka luasnya adalah 25 cm persegi.
- Persegi: Dikenal karena kesimetrisannya, persegi memiliki empat sisi yang sama panjang dan empat sudut siku-siku (90 derajat). Luas persegi dihitung dengan rumus
Luas = sisi
– sisi. Jika sisi persegi adalah 7 cm, maka luasnya adalah 49 cm persegi. Keunikan persegi terletak pada kesempurnaannya, yang membuatnya ideal dalam berbagai aplikasi, mulai dari desain arsitektur hingga komputasi.
- Lingkaran: Bangun datar yang sempurna, dengan setiap titik pada kelilingnya berjarak sama dari pusat. Hubungan antara jari-jari (r), diameter (d), dan keliling (K) sangat penting. Luas lingkaran dihitung dengan rumus
Luas = π
– r 2, di mana π (pi) adalah konstanta matematika (sekitar 3.14159). Jika jari-jari lingkaran adalah 4 cm, maka luasnya adalah sekitar 50.27 cm persegi.
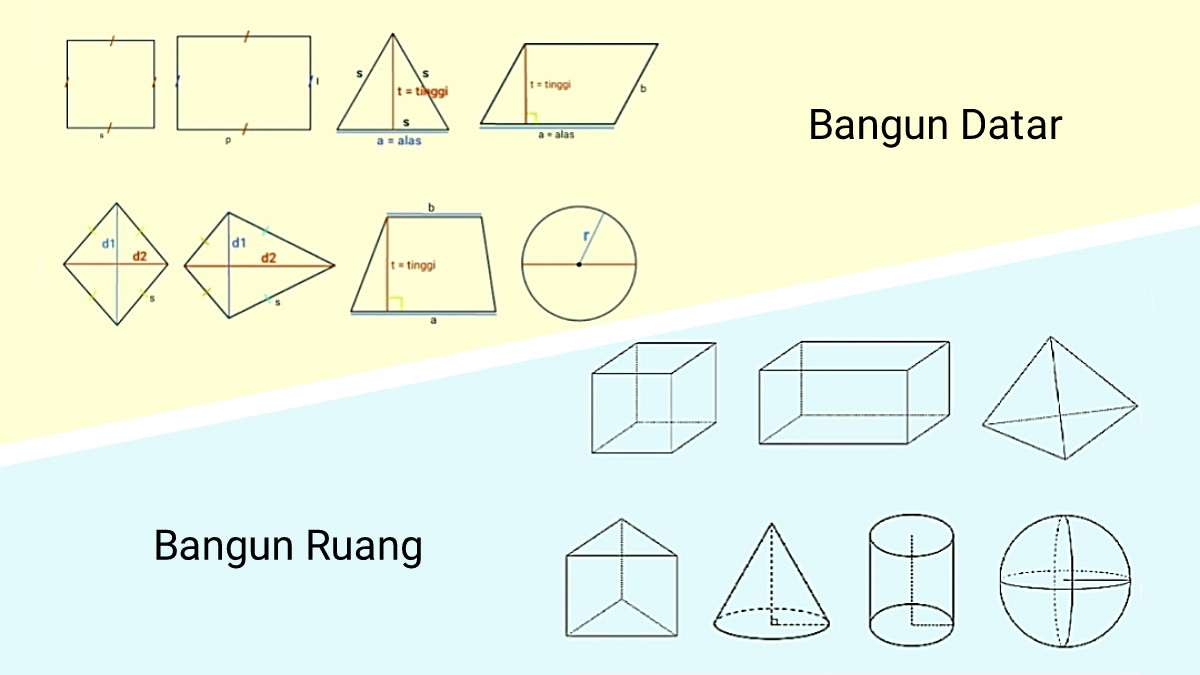
Rumus Luas dan Keliling Bangun Datar
Rumus adalah bahasa universal dalam matematika. Tabel berikut merangkum rumus-rumus penting untuk menghitung luas dan keliling berbagai jenis bangun datar:
| Nama Bangun | Rumus Luas | Rumus Keliling | Contoh Penggunaan |
|---|---|---|---|
| Persegi Panjang | Panjang x Lebar | 2 x (Panjang + Lebar) | Menghitung luas dan keliling halaman rumah. |
| Segitiga | 1/2 x Alas x Tinggi | Jumlah Sisi | Menghitung luas atap rumah. |
| Lingkaran | π x r2 | 2 x π x r | Menghitung luas dan keliling kolam renang berbentuk lingkaran. |
| Jajar Genjang | Alas x Tinggi | 2 x (Sisi 1 + Sisi 2) | Menghitung luas lahan pertanian. |
| Trapesium | 1/2 x (Sisi 1 + Sisi 2) x Tinggi | Jumlah Sisi | Menghitung luas penampang sungai. |
Simetri, Konveksitas, dan Penyelesaian Masalah Geometri
Sifat-sifat seperti simetri dan konveksitas memainkan peran penting dalam memecahkan masalah geometri. Simetri memungkinkan kita untuk membagi bangun menjadi bagian-bagian yang identik, menyederhanakan perhitungan dan analisis. Konveksitas, yang berarti bahwa setiap garis yang menghubungkan dua titik di dalam bangun tetap berada di dalam bangun, memengaruhi cara kita memahami bentuk dan ruang. Contohnya, dalam desain arsitektur, simetri sering digunakan untuk menciptakan keseimbangan visual dan stabilitas struktural.
Konveksitas memastikan bahwa sebuah objek dapat diakses dari semua sisi, penting dalam perencanaan tata ruang.
Mari kita mulai petualangan belajar ini! Pernahkah terpikir olehmu, istilah apa yang digunakan untuk menyebut gaya kupu-kupu dalam dunia renang? Sungguh menarik, bukan? Kemudian, jika kamu ingin memahami fenomena alam atau sosial, jangan lewatkan contoh teks eksplanasi yang akan membantumu merangkai informasi. Jangan lupakan juga keajaiban gerak pada tumbuhan , yang mengajarkan kita tentang ketahanan hidup.
Akhirnya, mari kita dengarkan irama indah dari alat musik dari Maluku , yang akan menginspirasi kita semua.
Ilustrasi Sifat-Sifat Khusus Bangun Datar
Bayangkan sebuah ilustrasi yang menampilkan:
- Persegi: Ditampilkan dengan sudut-sudut siku-siku yang jelas, menekankan kesempurnaan geometrisnya.
- Lingkaran: Diilustrasikan dengan jari-jari yang memancar dari pusat ke berbagai titik pada keliling, menyoroti konsep jarak yang sama.
- Segitiga: Menampilkan garis tinggi yang tegak lurus dengan alas, menunjukkan hubungan antara alas, tinggi, dan luas.
Ilustrasi ini tidak hanya memvisualisasikan sifat-sifat unik bangun datar, tetapi juga menginspirasi pemahaman yang lebih mendalam tentang bagaimana mereka berinteraksi dalam ruang.
Pandangan dari Berbagai Sumber, Apakah yang dimaksud bangun datar
Berikut adalah kutipan yang menunjukkan pentingnya pemahaman sifat-sifat bangun datar:
“Pemahaman mendalam tentang geometri, termasuk sifat-sifat bangun datar, adalah fondasi penting dalam pengembangan teknologi modern.”
(Sumber
Journal of Engineering Education)
“Sifat-sifat bangun datar memberikan dasar untuk memahami konsep-konsep matematika yang lebih kompleks, yang sangat penting dalam bidang sains dan rekayasa.”(Sumber
Mathematics Education Review)
“Kemampuan untuk mengidentifikasi dan memanfaatkan sifat-sifat bangun datar adalah keterampilan penting dalam pemecahan masalah di berbagai bidang, mulai dari arsitektur hingga desain grafis.”(Sumber
Design Quarterly)
Penerapan Praktis: Apakah Yang Dimaksud Bangun Datar
Source: cilacapklik.com
Bangun datar, lebih dari sekadar bentuk geometris di buku pelajaran, adalah fondasi tak kasat mata yang membentuk dunia di sekitar kita. Kehadirannya begitu fundamental sehingga kita seringkali tak menyadari betapa luas dan mendalamnya pengaruh mereka. Dari gedung pencakar langit yang menjulang hingga desain logo yang memikat, konsep bangun datar berperan penting dalam menciptakan keseimbangan antara estetika dan fungsionalitas.
Mari kita selami bagaimana konsep-konsep ini hidup dan bernapas dalam berbagai aspek kehidupan, membuktikan bahwa matematika bukanlah sesuatu yang terisolasi, melainkan alat yang ampuh untuk membentuk, merancang, dan membangun peradaban.
Penerapan dalam Berbagai Bidang
Konsep bangun datar menemukan aplikasi yang tak terhitung jumlahnya dalam berbagai disiplin ilmu. Dalam arsitektur, misalnya, persegi panjang, segitiga, dan lingkaran digunakan untuk merancang denah, fasad, dan struktur bangunan secara keseluruhan. Rekayasa memanfaatkan bangun datar untuk menghitung kekuatan material, menganalisis distribusi beban, dan memastikan stabilitas struktur. Di dunia seni, bangun datar menjadi elemen dasar dalam komposisi lukisan, patung, dan instalasi artistik.
Desainer grafis menggunakan bangun datar untuk menciptakan logo, ilustrasi, dan tata letak yang menarik secara visual.
Sebagai contoh, perhatikan bagaimana The Shard di London, dengan fasad segitiganya yang khas, memanfaatkan konsep segitiga untuk mencapai stabilitas struktural dan tampilan yang ikonik. Atau, perhatikan bagaimana logo-logo terkenal seperti logo Apple yang berbentuk persegi panjang atau logo Adidas yang menggunakan tiga garis paralel yang membentuk segitiga, menggunakan bangun datar untuk menyampaikan identitas merek. Di bidang rekayasa, jembatan gantung seringkali mengadopsi bentuk parabola, yang didasarkan pada konsep bangun datar, untuk mendistribusikan beban secara merata dan efisien.
Dalam seni, karya-karya Piet Mondrian, dengan penggunaan garis horizontal dan vertikal yang membentuk persegi panjang dan persegi, adalah contoh nyata bagaimana bangun datar dapat digunakan untuk menciptakan komposisi yang kompleks dan bermakna.
Proyek-Proyek Nyata yang Menggunakan Bangun Datar
Pemahaman tentang bangun datar adalah kunci dalam keberhasilan banyak proyek ikonik. Berikut adalah beberapa contoh yang menakjubkan:
- Gedung Opera Sydney: Struktur atapnya yang unik terdiri dari segmen-segmen yang membentuk bentuk seperti cangkang, yang merupakan variasi dari bangun datar.
- Piramide Giza: Bentuk piramida yang megah dibangun berdasarkan konsep segitiga dan persegi, mencerminkan presisi geometri yang luar biasa.
- Jembatan Golden Gate: Bentuk lengkung parabola pada kabel gantung jembatan merupakan aplikasi langsung dari konsep bangun datar.
- Logo Perusahaan Terkenal: Banyak logo perusahaan terkenal, seperti Nike (centang), McDonald’s (lengkungan emas), dan Google (bentuk huruf), mengandalkan bangun datar untuk menciptakan identitas visual yang kuat.
Penggunaan dalam Perhitungan dan Perencanaan
Konsep bangun datar sangat penting dalam perhitungan luas lahan, perencanaan tata ruang, dan desain produk. Dalam perhitungan luas lahan, bangun datar seperti persegi, persegi panjang, segitiga, dan lingkaran digunakan untuk menghitung luas bidang tanah yang tidak beraturan. Dalam perencanaan tata ruang, bangun datar digunakan untuk merancang tata letak bangunan, jalan, dan ruang terbuka hijau. Dalam desain produk, bangun datar digunakan untuk merancang bentuk dan ukuran produk, serta untuk menghitung volume dan kapasitas.
Sebagai contoh, dalam perencanaan tata ruang sebuah kota, para perencana menggunakan bangun datar untuk menentukan ukuran dan bentuk blok perumahan, jalan, dan taman. Mereka juga menggunakan konsep bangun datar untuk menghitung luas lahan yang dibutuhkan untuk berbagai fasilitas umum, seperti sekolah, rumah sakit, dan pusat perbelanjaan. Dalam desain produk, seorang desainer dapat menggunakan bangun datar untuk merancang bentuk sebuah meja, kursi, atau peralatan elektronik.
Dengan memahami konsep bangun datar, desainer dapat menciptakan produk yang tidak hanya estetis tetapi juga fungsional dan efisien.
Ilustrasi dalam Desain Visual
Bangun datar memainkan peran krusial dalam desain logo, ilustrasi, dan representasi visual lainnya. Mereka memberikan dasar untuk menciptakan bentuk, komposisi, dan proporsi yang menarik secara visual. Penggunaan bangun datar dalam desain seringkali bertujuan untuk menyampaikan pesan tertentu, menciptakan identitas merek, atau mengkomunikasikan informasi secara efektif.
Sebagai contoh, logo perusahaan seringkali menggunakan bangun datar untuk menciptakan kesan yang kuat dan mudah diingat. Bentuk geometris seperti lingkaran, persegi, dan segitiga sering digunakan karena mereka memiliki makna simbolis yang berbeda. Lingkaran dapat melambangkan kesatuan dan keutuhan, persegi dapat melambangkan stabilitas dan keandalan, sementara segitiga dapat melambangkan pertumbuhan dan perubahan. Ilustrasi juga sering menggunakan bangun datar untuk menciptakan bentuk dan karakter.
Seorang ilustrator dapat menggunakan lingkaran, persegi, dan segitiga untuk membangun bentuk dasar dari sebuah karakter, kemudian menambahkan detail untuk menciptakan tampilan yang unik. Representasi visual lainnya, seperti diagram dan grafik, juga menggunakan bangun datar untuk mengkomunikasikan informasi secara visual. Diagram lingkaran digunakan untuk menunjukkan proporsi, sedangkan grafik batang dan garis digunakan untuk menunjukkan tren dan perbandingan.
Studi Kasus: Pembangunan Struktur Arsitektur
Mari kita telusuri penerapan konsep bangun datar dalam pembangunan sebuah struktur arsitektur, misalnya, sebuah rumah modern dengan desain minimalis. Prosesnya melibatkan beberapa langkah kunci:
- Perencanaan Denah: Desainer memulai dengan membuat denah rumah, yang merupakan representasi dua dimensi dari tata letak ruangan. Bangun datar seperti persegi panjang dan persegi digunakan untuk menentukan ukuran dan bentuk setiap ruangan, seperti kamar tidur, ruang tamu, dan dapur.
- Perhitungan Luas dan Volume: Setelah denah selesai, langkah selanjutnya adalah menghitung luas setiap ruangan dan volume total rumah. Konsep bangun datar digunakan untuk menghitung luas lantai, luas dinding, dan volume ruangan. Perhitungan ini penting untuk menentukan kebutuhan material, seperti jumlah bata, kayu, dan cat yang dibutuhkan.
- Desain Fasad: Fasad rumah, atau tampilan eksterior, dirancang dengan mempertimbangkan estetika dan fungsionalitas. Bangun datar seperti persegi, persegi panjang, dan segitiga digunakan untuk merancang bentuk jendela, pintu, dan atap. Desainer juga mempertimbangkan proporsi dan keseimbangan visual untuk menciptakan tampilan yang menarik.
- Analisis Struktur: Untuk memastikan stabilitas struktur, insinyur sipil melakukan analisis struktural. Mereka menggunakan konsep bangun datar untuk menghitung beban yang bekerja pada struktur, seperti beban mati (berat struktur itu sendiri), beban hidup (berat penghuni dan perabotan), dan beban angin. Analisis ini membantu menentukan ukuran dan jenis material yang dibutuhkan untuk membangun rumah.
- Pelaksanaan Konstruksi: Selama proses konstruksi, tukang bangunan menggunakan konsep bangun datar untuk memotong dan memasang material, seperti dinding, lantai, dan atap. Mereka menggunakan alat ukur, seperti penggaris dan meteran, untuk memastikan bahwa semua elemen dibangun sesuai dengan rencana.
Studi kasus ini menyoroti bagaimana konsep bangun datar tidak hanya penting dalam desain arsitektur, tetapi juga dalam perencanaan, perhitungan, dan pelaksanaan konstruksi. Pemahaman yang mendalam tentang konsep ini memastikan bahwa struktur yang dibangun tidak hanya indah secara visual, tetapi juga aman, stabil, dan fungsional.
Penutupan
Source: z-dn.net
Memahami bangun datar bukan hanya tentang menghafal rumus atau menggambar bentuk. Ini tentang melihat dunia dengan cara baru, mengapresiasi keindahan matematika dalam segala hal. Dengan pengetahuan ini, seseorang dapat menjelajahi dunia arsitektur, seni, teknologi, dan banyak lagi dengan lebih percaya diri dan kreatif.
Jadi, mari terus belajar dan bereksplorasi. Karena di balik setiap garis, sudut, dan kurva, terdapat potensi tak terbatas untuk inovasi dan pemahaman. Bangun datar bukan hanya pelajaran, melainkan sebuah perjalanan yang tak pernah berakhir.